Question

The supervisor of a production line wants to check if the average time to assemble an electronic component is different from 14 minutes. Assume that the population of assembly time is normally distributed with a standard deviation of 3.4 minutes. The supervisor times the assembly of 14 components, and finds that the average time for completion is 11.6 minutes. How would you calculate the p-value for the hypothesis test

Answer 1

The p-value for the hypothesis test is 0.0042.

Explanation:

We are given that the supervisor of a production line wants to check if the average time to assemble an electronic component is different from 14 minutes.

Assume that the population of assembly time is normally distributed with a standard deviation of 3.4 minutes. The supervisor times the assembly of 14 components, and finds that the average time for completion is 11.6 minutes.

Let
`\mu` = average time to assemble an electronic component.

SO, Null Hypothesis,
`H_0` :
`\mu` = 14 minutes {means that the average time to assemble an electronic component is equal to 14 minutes}

Alternate Hypothesis,
`H_A` :
`\mu`
`\\eq` 14 minutes {means that the average time to assemble an electronic component is different from 14 minutes}

The test statistics that will be used here is One-sample z test statistics as we know about the population standard deviation;

T.S. =
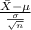`(\bar X -\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample average time for completion = 11.6 minutes

`\sigma` = population standard deviation = 3.4 minutes

n = sample of components = 14

So, test statistics =
`(11.6-14)/((3.4)/(√(14) ) )`

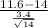
= -2.64

Now, P-value of the hypothesis test is given by the following formula;

P-value = P(Z < -2.64) = 1 - P(Z
`\leq` 2.64)

= 1 - 0.99585 = 0.0042

Hence, the p-value for the hypothesis test is 0.0042.