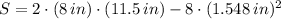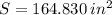Answer:
1)
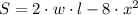 , 2) The domain of S is
, 2) The domain of S is
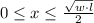 . The range of S is
. The range of S is
 , 3)
, 3)
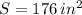 , 4)
, 4)
 , 5)
, 5)
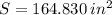
Explanation:
1) The function of the box is:
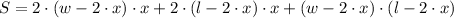

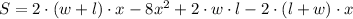
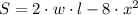
2) The maximum cutout is:
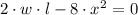
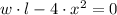
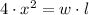
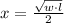
The domain of S is
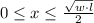 . The range of S is
. The range of S is

3) The surface area when a 1'' x 1'' square is cut out is:
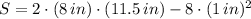
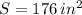
4) The size is found by solving the following second-order polynomial:


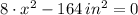

5) The equation of the box volume is:
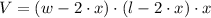
![V = [w\cdot l -2\cdot (w+l)\cdot x + 4\cdot x^(2)]\cdot x](https://img.qammunity.org/2021/formulas/mathematics/college/od4av4rv1f6pjff553id30aihaj5pbur7s.png)
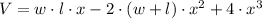
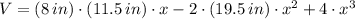

The first derivative of the function is:

The critical points are determined by equalizing the derivative to zero:
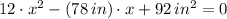
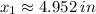

The second derivative is found afterwards:
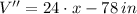
After evaluating each critical point, it follows that
 is an absolute minimum and
is an absolute minimum and
 is an absolute maximum. Hence, the value of the cutoff so that volume is maximized is:
is an absolute maximum. Hence, the value of the cutoff so that volume is maximized is:
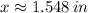
The surface area of the box is: