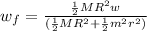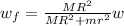Question

Problem: A disk of mass m and radius r is initially held at rest just above a larger disk of mass M and radius R that is rotating at angular speed wi. What is the final angular speed of the disks after the top one is dropped onto the bottom one and they stop slipping on each other? Note: the moment of inertia of a disk of mass M and radius R about an axis through its center and perpendicular to the disk is I = (1/2)MR2.

Answer 1

The final angular velocity is
`w_f = (MR^2)/(MR^2+ mr^2) w`

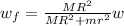
Step-by-step explanation:

From the question we are told that

The mass of the first disk is m

The radius of the first disk is r

The mass of second disk is M

The radius of second disk is R

The speed of rotation is w

The moment of inertia of second disk is
`I = (1)/(2) MR^2`

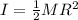
Since the first disk is at rest initially

The initial angular momentum would be due to the second disk and this is mathematically represented as

`L_i = Iw = (1)/(2) MR^2 w`

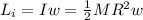
Now when the first disk is then dropped the angular momentum of the whole system now becomes

`L_f = (I_1 + I_2 ) w_f= ( (1)/(2) MR^2 + (1)/(2) m^2 r^2) w_f`

This above is because the formula for moment of inertia is the same for every disk

According to the law conservation of angular momentum

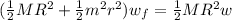
`L_f = L_i`

`( (1)/(2) MR^2 + (1)/(2) m^2 r^2) w_f = (1)/(2) MR^2 w`

=>
`w_f = ((1)/(2) MR^2 w )/(( (1)/(2) MR^2 + (1)/(2) m^2 r^2))`

`w_f = (MR^2)/(MR^2+ mr^2) w`