Question

Two scales on a nondigital voltmeter measure voltages up to 20.0 and 30.0 V, respectively. The resistance connected in series with the galvanometer is 1680 Ω for the 20.0-V scale and 2930 Ω for the 30.0-V scale. Determine the coil resistance.

Answer 1

Resistance of the circuit is 820 Ω

Step-by-step explanation:

Given:

Two galvanometer resistance are given along with its voltages.

Let the resistance is "R" and the values of voltages be 'V' and 'V1' along with 'G' and 'G1'.

⇒
`V=20\ \Omega,\ V_1=30\ \Omega`

⇒
`G=1680\ \Omega,\ G_1=2930\ \Omega`

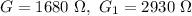
Concept to be used:

Conversion of galvanometer into voltmeter.

Let
`G` be the resistance of the galvanometer and
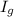`I_g` the maximum deflection in the galvanometer.

To measure maximum voltage resistance
`R` is connected in series .

So,

⇒
`V=I_g(R+G)`

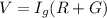
We have to find the value of
`R` we know that in series circuit current are same.

For
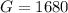`G=1680` For
`G_1=2930`

⇒
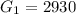
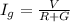`I_g=(V)/(R+G)` equation (i) ⇒
`I_g=(V_1)/(R+G_1)` equation (ii)

Equating both the above equations:

⇒
`(V)/(R+G) = (V_1)/(R+G_1)`

⇒
`V(R+ G_1) = V_1 (R+G)`

⇒
`VR+VG_1 = V_1R+V_1G`

⇒
`VR-V_1R = V_1G-VG_1`

⇒
`R(V-V_1) = V_1G-VG_1`

⇒
`R =(V_1G-VG_1)/((V-V_1))`

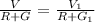
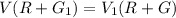
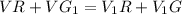
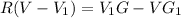
⇒ Plugging the values.

⇒
`R =((30* 1680) - (20* 2930))/((20-30))`

⇒
`R =((50400 - 58600))/((-10))`

⇒
`R=(-8200)/(-10)`

⇒
`R=820\ \Omega`

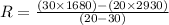
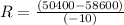
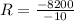
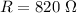
The coil resistance of the circuit is 820 Ω .