Answer:
The 95% confidence interval for the difference in population proportions who returned home after spring break is (0.31, 0.61).
Explanation:
The (1 - α)% confidence interval for the difference between two population proportions is:
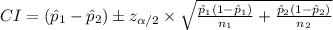
The information provided is:
Stayed Returned
1st year 19 68
4th year 36 17
Compute the sample proportion of 1st year students who returned home as follows:

Compute the sample proportion of 4th year students who returned home as follows:
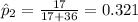
The critical value of z for 95% confidence level is:
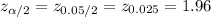
Compute the 95% confidence interval for the difference between two proportions as follows:
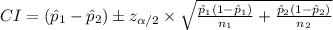

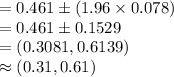
Thus, the 95% confidence interval for the difference in population proportions who returned home after spring break is (0.31, 0.61).
The 95% confidence interval for difference between two population proportions, (0.31, 0.61) implies that there is a 0.95 probability that the true difference between the proportions is included in the interval.