Answer:
the workdone = 4420.78 J
Step-by-step explanation:
The work done raising the rope.
Mass of the rope in the i-th subinterval is 0.8Δh and the work done raising this to the top is :
0.8Δh × 9.8 ×(13 -hi)
= 7.84 (13-hi) Δh
The total work done raising the rope is thus illustrated as :
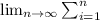
7.84 (13-hi) Δh
∫ 7.84 (13-hi) dh (from 0 to 13)
= -7.84 (1/2)(13 - h)² (from 0 to 13)
= 662.48 J
The mass of the water mi at height hi is given as mi = 39 - 3hi &
the workdone raising this through the distance Δh is 9.8(39 - 3hi)Δh
Thus, the total work done raising the water is :
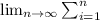
9.8(39 - 3hi)Δh
∫ 9.8 (39 - 3h) (from 0 to 13)
= -9.8 (1/6) (39 -3 h)² (from 0 to 13)
= 2484.30 J
The work done raising the bucket is 10 × 13 ×9.8 = 1274 J ,
The total work in raising the rope and the bucket of water is (1274 + 662.48 + 2484.30) J
= 4420.78 J
Thus, the workdone = 4420.78 J