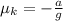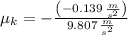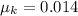Answer:
a)
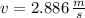 , b)
, b)
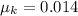
Step-by-step explanation:
a) The final speed is determined by the Principle of Momentum Conservation:
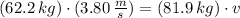
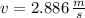
b) The deceleration experimented by the system person-sled is:
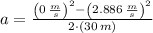
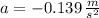
By using the Newton's Laws, the only force acting on the motion of the system is the friction between snow and sled. The kinetic coefficient of friction is: