Answer:
The intensity on a screen 70 ft from the light is 1.728 foot candle.
Explanation:
Given that,
The magnitude of intensity
 of light varies inversely as the square of the magnitude of distance D from the source.
of light varies inversely as the square of the magnitude of distance D from the source.
That is
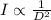
Then,
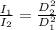
Given that,
The magnitude of intensity of illumination on a screen 56 ft from a light is 2.7 foot-candle.
Here,
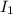 =2.7 foot-candle,
=2.7 foot-candle,
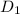 = 56 ft
= 56 ft
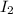 =?,
=?,
 = 70 ft.
= 70 ft.
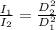
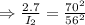
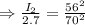

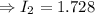 foot-candle
foot-candle
The intensity on a screen 70 ft from the light is 1.728 foot candle.