Question

The product of two consecutive odd integers is 1 less than twice their sum. Find the integers.

Answer 1

Two consecutive odd integers are
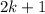`2k+1` and
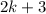`2k+3`, for some integer
`k`.

Their product is
`(2k+1)(2k+3)=4k^2+8k+3`.

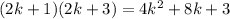Twice their sum is
`2(2k+1+2k+3)=2(4k+4)=8k+8`

Since the product is 1 less than twice the sum, we have

`\underbrace{4k^2+8k+3}_{\text{the product}}=\underbrace{8k+8}_{\text{twice the sum}}-1`

So, we have

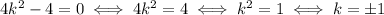
`4k^2-4=0 \iff 4k^2=4 \iff k^2=1 \iff k=\pm 1`

If
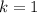`k=1`, the integers are 3 and 5

If
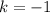`k=-1`, the integers are -1 and 1.

In both cases, in fact, we have:

• 3*5 = 15, which is one less than 2(3+5)=2*8=16
• (-1)*1=-1, which is one less than 2(-1+1)=0