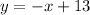Question

What is the relationship between x and y

Answer 1

Given:

Given that the table with values of x and y.

We need to determine the relationship between x and y.

Slope:

The slope of the relation can be determined using the formula,

`m=(y_2-y_1)/(x_2-x_1)`

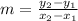
Substituting the points (2,11) and (4,9), we get;

`m=(9-11)/(4-2)`

`m=(-2)/(2)`

`m=-1`

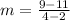
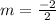
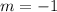
Thus, the slope of the relation is m = -1.

y - intercept:

The y - intercept of the relation is the value of y when x = 0.

Hence, from the table, it is obvious that when x = 0, the value of y is 13.

Thus, the y - intercept of the relation is b = 13.

Relationship between x and y:

The relationship between x and y can be determined using the formula,

`y=mx+b`

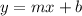
Substituting m = -1 and y =13, we get;

`y=-x+13`

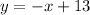
Thus, the relationship between x and y is
`y=-x+13`