In order to define a function, you need two sets, say
 and
and
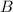 .
.
 will be the domain, i.e. the "starting" set.
will be the domain, i.e. the "starting" set.
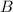 will be the range (or co-domain), and you can think of this as the "landing" set.
will be the range (or co-domain), and you can think of this as the "landing" set.
A function is a rule that maps, following the same logic, every element of
 into one and only one elment of
into one and only one elment of
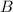 .
.
Most of the time, you'll deal with numeric function, i.e. functions that take a number as input and give another number as output. For example, writing

means that your function takes a certain number
 as input, and return twice that number,
as input, and return twice that number,
 , as output.
, as output.
Finally, a function can also be described by explicit pair of inputs and outputs. For example, defining a function
 with the table
with the table

means that
 maps 1 onto 2, 4 onto 6 and 7 onto 89. Such a collection of pairs is actually a function if:
maps 1 onto 2, 4 onto 6 and 7 onto 89. Such a collection of pairs is actually a function if:
- Every point in the domain is actually associated with an output in the range (1)
- Every point in the domain is associated with only one output in the range (2)
(1) for example, if your domain is
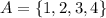 , and the range is
, and the range is
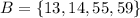 , the table
, the table
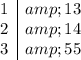
does not represent a function from
 to
to
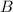 , because 4 is in the domain, but it is not mapped into anything. Similarly, the table
, because 4 is in the domain, but it is not mapped into anything. Similarly, the table

is not a valid function, because 4 is mapped onto 89, which is not in the range.
(2) for example, using the same sets as above, the table

does not represent a function from
 to
to
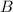 , because 1 is mapped into both 13 and 14, but a value in the domain can be mapped into only one value in the range.
, because 1 is mapped into both 13 and 14, but a value in the domain can be mapped into only one value in the range.