Question

Find the value of t, rounded to the nearest tenth

Answer 1

Given:

Given that RST is a right triangle.

The measure of ∠R is 35°.

The length of ST is 12 units.

The length of the hypotenuse is t units.

We need to determine the value of t.

Value of t:

The value of t can be determined using the trigonometric ratio.

Thus, we have;

`sin \ \theta=(opp)/(hyp)`

where
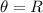`\theta=R`, the side opposite to ∠R is ST and hypotenuse is SR.

Substituting these values, we get;

`sin \ R=(ST)/(SR)`

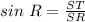
Substituting ST = 12 and SR = t, we get;

`sin \ 35^(\circ)=(12)/(t)`

Simplifying, we get;

`t=(12)/(sin \ 35^(\circ))`

`t=(12)/(0.574)`

`t=20.9`

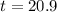
Thus, the value of t is 20.9 units.