Answer:
The colony size after 4 days is 10 497.
There will be at least 90 000 mosquitoes on the 8th day.
Explanation:
Size of colony after 4 days
The law of uninhibited growth means the mosquitoes will increase using this formula for exponential growth:
y = abˣ
"y" is the total population after "x" time
"a" is the initial population
"b" is the rate of growth or decay
Initial population a = 1000
Rate of change
b = 1800/1000
b = 1.8 A positive rate of change means growth
The time passed is 4 days, x = 4
Substitute the values and find "y" for the population after 4 days:
y = abˣ
y = (1000)(1.8)⁴ Do the exponent first
y = (1000)(10.4976) Multiply
y = 10497.6
We can't have 0.6 of a mosquito, so the population is y = 10 497.
Time until 90 000 mosquitoes
If we want to find "x" (time) until y = 90 000, substitute the same "a" and "b" values. The rate of change and starting population are the same. Then, isolate "x".
y = abˣ
90 000 = (1000)(1.8)ˣ
90000 / 1000 = 1.8ˣ Divide both sides by 1000
90 = 1.8ˣ
We can find "x" by trial and error or using "log" on the calculator. I will use log.
x =
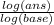
The base is 1.8, and "ans" (answer) is 90.
x =
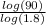
x ≈ 7.65515....
On the seventh day, you will not have 90 000 mosquitoes yet. You have to wait until the next day.
You also can't use a decimal number because you don't know when the mosquitoes are born during day 7.
x ≈ 8
Therefore, it will be 8 days until there are 90 000 mosquitoes.