1 Answer

Lilibeth · Answer 1 · 2021-09-18T07:41:05+0000

Answer:

(a) The 80% confidence interval for the population mean nitrate concentration is (0.648, 0.692).

(b) The critical value of t that should be used in constructing the 80% confidence interval is 1.345.

Explanation:

Let X = nitrate concentration.

The sample mean nitrate concentration is,
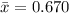$\bar x=0.670$ cc/cubic meter.

The sample standard deviation of the nitrate concentration is,
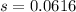s=0.0616 .

It assumed that the population is approximately normal.

And since the population standard deviation is not known, we will use a t-interval.

The (1 - α)% confidence interval for population mean (μ) is:

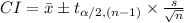
$CI=\bar x\pm t_(\alpha/2, (n-1))* (s)/(√(n))$

(a)

The critical value of t for α = 0.20 and degrees of freedom, (n - 1) = 14 is:

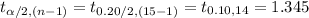
$t_(\alpha/2, (n-1))=t_(0.20/2, (15-1))=t_(0.10, 14)=1.345$

*Use a t-table for the critical value.

Compute the 80% confidence interval for the population mean nitrate concentration as follows:

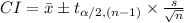
$CI=\bar x\pm t_(\alpha/2, (n-1))* (s)/(√(n))$

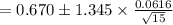
$=0.670\pm 1.345* (0.0616)/(√(15))$

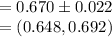
$=0.670\pm 0.022\\=(0.648, 0.692)\\$

Thus, the 80% confidence interval for the population mean nitrate concentration is (0.648, 0.692).

(b)

The critical value of t for confidence level (1 - α)% and (n - 1) degrees of freedom is:

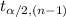
$t_(\alpha/2, (n-1))$

The value of is:

α = 0.20

And the degrees of freedom is,

(n - 1) = 15 - 1 = 14

Compute the critical value of t for confidence level 80% and 14 degrees of freedom as follows:

$t_(\alpha/2, (n-1))=t_(0.20/2, (15-1))$

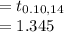
$=t_(0.10, 14)\\=1.345$

*Use a t-table for the critical value.

Thus, the critical value of t that should be used in constructing the 80% confidence interval is 1.345.

Please log in or register to add a comment.