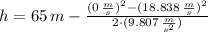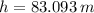Answer:
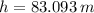
Step-by-step explanation:
The speed of the firework shell just before the explosion is:
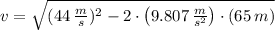

After the explosion, the initial speed of one of the mass halves is:
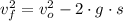
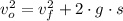
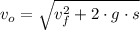
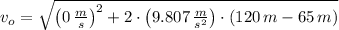

The initial speed of the other mass half is determined from the Principle of Momentum Conservation:

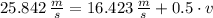
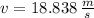
The height reached by this half is: