Answer:
The common difference equals:
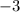
The sum of the sequence equals:
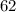
The explicit formula of this sequence is:
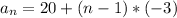
The recursive formula of this sequence is:
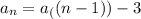
The nth terms:
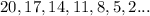
Explanation:
An arithmetic sequence, or arithmetic progression, is a set of numbers in which the difference between consecutive terms (terms that come after one another) is constant. This difference is called the common difference.
1. Find the common difference.
Find the common difference by subtracting any term in the sequence from the term that comes after it.
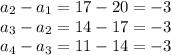
The difference of the sequence is constant and equals the difference between two consecutive terms.
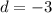
2. Find the sum.
Calculate the sum of the sequence using the sum formula:
Formula
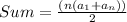
Plug in terms
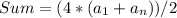
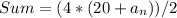
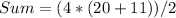
Simplify the expression
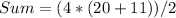
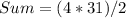
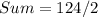
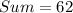
The sum of this sequence is
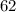 .
.
This series corresponds to the following straight line
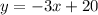
3. Find the explicit form.
The formula for expressing arithmetic sequences in their explicit form is:
Formula:
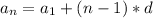
Plug in the terms.
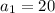 (this is the 1st term)
(this is the 1st term)
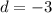 (this is the common difference)
(this is the common difference)
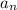 (this is the nth term)
(this is the nth term)
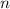 (this is the term position)
(this is the term position)
The explicit form of this arithmetic sequence is:
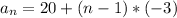
4. Find the recursive form.
The formula for expressing arithmetic sequences in their recursive form is:
Formula:
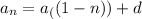
Plug in the d term.
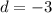 (this is the common difference)
(this is the common difference)
The recursive form of this arithmetic sequence is:
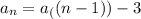
5. Find the nth element.
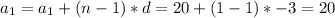
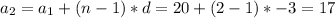
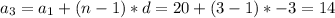
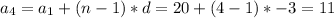
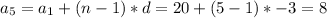
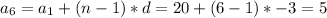
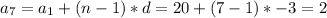
Terms and topics: