Question

Penalty Shots in World Cup Soccer A study1 of 138 penalty shots in World Cup Finals games between 1982 and 1994 found that the goalkeeper correctly guessed the direction of the kick only 41% of the time. The article notes that this is ‘‘slightly worse than random chance." We use these data as a sample of all World Cup penalty shots ever. Test at a 5% significance level to see whether there is evidence that the percent guessed correctly is less than 50%. The sample size is large enough to use the normal distribution. The standard error from a randomization distribution under the null hypothesis is SE=0.043. 1St.John, A., ‘‘Physics of a World Cup Penalty-Kick Shootout - 2010 World Cup Penalty Kicks," Popular Mechanics, June 14, 2010.

Answer 1

There is enough evidence to support the claim that the percent that the goalkeeper guessed correctly is less than 50%.

Explanation:

We have to perform an hypothesis test on a proportion.

We have a sample of size n=138, a sample mean of p=0.41.

The standard error is SE=0.043.

We want to test the claim that the real proportion is below 50%.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.5\\\\H_a: \pi<0.5`

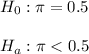
The significance level is α=0.05.

The z-statistic can be calculated as:

`z=(p-\pi+0.5/n)/(\sigma_p)=(0.41-0.5+0.5/138)/(0.043)=(-0.086)/(0.043)= -2`

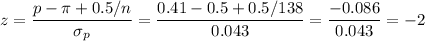
The P-value (left tail test) for this z-statistic is:

`P-value=P(z<-2)=0.023`

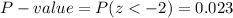
The P-value is smaller than the level of significance, so the effect is significant. The null hypothesis is rejected.

There is enough evidence to support the claim that the percent that the goalkeeper guessed correctly is less than 50%.