Answer:
1. Null Hypothesis,
 :
:
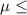 70 mph
70 mph
Alternate Hypothesis,
 :
:
 > 70 mph
> 70 mph
2. Value of test statistics is 2.652.
Explanation:
We are given that Kansas Highway Patrol recorded the speed of 450 interstate vehicles and found the mean speed of 70.2 mph with standard deviation 1.6 mph.
We have to conduct a hypothesis test at significance level 0.01 to decide whether or not to reduce the money sent to Kansas.
Let
 = true mean speed of all vehicles on the Kansas interstate highway system.
= true mean speed of all vehicles on the Kansas interstate highway system.
SO, Null Hypothesis,
 :
:
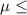 70 mph {means that the federal government will not reduce the amount of funding it provides as the speed limit is less than or equal to 70 mph}
70 mph {means that the federal government will not reduce the amount of funding it provides as the speed limit is less than or equal to 70 mph}
Alternate Hypothesis,
 :
:
 > 70 mph {means that the federal government will reduce the amount of funding it provides as the speed limit exceed 70 mph}
> 70 mph {means that the federal government will reduce the amount of funding it provides as the speed limit exceed 70 mph}
The test statistics that will be used here is One-sample t test statistics as we don't know about the population standard deviation;
T.S. =
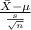 ~
~

where,
 = sample mean speed limit of 450 interstate vehicles = 70.2 mph
= sample mean speed limit of 450 interstate vehicles = 70.2 mph
s = sample standard deviation = 1.6 mph
n = sample of vehicles = 450
So, test statistics =
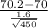 ~
~
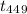
= 2.652
Hence, the value of test statistics is 2.652.