Question

Use StatKey or other technology to generate a bootstrap distribution of sample proportions and find the standard error for that distribution. Compare the result to the standard error given by the Central Limit Theorem, using the sample proportion as an estimate of the population proportion p.

Proportion of peanuts in mixed nuts, with n=94 and P =0.52
Round your answer for the bootstrap SE to two decimal places, and your answer for the formula SE to three decimal places.

Answer 1

0.0515

Explanation:

By the central limit theorem

when n increase distribution when data follows normal

Standard Error, SE of P is

`SE = \sqrt{(p(1-p))/(n) }`

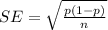
Bootstrap Standard Error =
`\sqrt{(p(1-p))/(n) }`

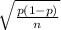
where n = 94 and p = 0.52

hence,

SE of Bootstrap =
`\sqrt{(0.52(1-0.52))/(94) }`

`=\sqrt{(0.2496)/(94) }\\\\=0.0515`

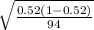
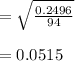
SE and the SE of Bootstrap are the same