Question

Cathy is asked to find the length of AC. She could use the Pythagorean Theorem and AC2 = 32 + 22. What other formula could she use? A) (0 + 3)2 - (1 + 3)2 B) (0 + 1)2 - (3 + 3)2 C) (0 - 3)2 + (1 - 3)2 D) (0 - 1)2 + (3 - 3)2

Answer 1

Cathy is asked to find the length of AC. She could use the Pythagorean Theorem and AC^2 = 3^2 + 2^2. What other formula could she use?

A) (0 + 3)^2 - (1 + 3)^2

B) (0 + 1)^2 - (3 + 3)^2

C) (0 - 3)^2 + (1 - 3)^2

D) (0 - 1)^2 + (3 - 3)^2

Option C is the right choice.

Explanation:

Given:

Cathy have used Pythagoras formula to find the hypotenuse.

Hypotenuse of the right angled triangle = AC

We know that:

In right angled triangle:

Hypotenuse square (h)^2 = Square of one side (p)^ + Square of another sides (b)^

⇒
`h^2=p^2+b^2`

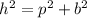
In Cathy's calculation:

⇒
`AC^2=3^2+2^2`

⇒
`AC^2=9+4`

⇒
`AC^2=13`

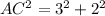
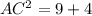
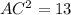
We have to look for another equation.

Lets see the options individually.

A.
`AC^2=(0 + 3)^2 - (1 + 3)^2= 9-16 = 7`

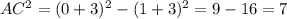
B.
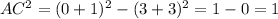
`AC^2=(0 + 1)^2 - (3 + 3)^2=1-0 =1`

C.
`AC^2=(0 - 3)^2 + (1 - 3)^2 =9+4=13`

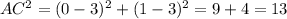
D.
`AC^2=(0 - 1)^2 + (3 - 3)^2=1+0 =1`

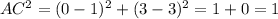
So,

The other formula Cathy can use is, C i.e. (0 - 3)^2 + (1 - 3)^2 .

Option C is the right choice.