Question

Based on the graph of an exponential function f(x)=b^x, for b >0, describe how you can verify that the output of the function can NEVER be equal to zero.

Answer 1

see the explanation

Explanation:

we know that

The equation of a exponential growth function is given by

`f(x)=a(b^x)`

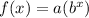
where

a is the initial value or y-intercept

b is the factor growth (b>0)

In this problem

a=1

so

`f(x)=b^x`

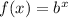
we know that

The graph of the function has no x-intercept

Remember that the x-intercept of a function is the value of x when the value of the function is equal to zero

That means ----> The output of the function can NEVER be equal to zero

Verify

For f(x)=0

`0=b^x`

Apply log both sides

`log(0)=xlog(b)`

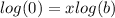
Remember that

log 0 is undefined. It's not a real number, because you can never get zero by raising anything to the power of anything else.