Answer:
(1) The probability that the sample percentage indicating global warming is having a significant impact on the environment will be between 64% and 69% is 0.3674.
(2) The two population percentages that will contain the sample percentage with probability 90% are 0.57 and 0.73.
(3) The two population percentages that will contain the sample percentage with probability 95% are 0.55 and 0.75.
Step-by-step explanation:
Let X = number of senior professionals who thought that global warming is having a significant impact on the environment.
The random variable X follows a Binomial distribution with parameters n = 100 and p = 0.65.
But the sample selected is too large and the probability of success is close to 0.50.
So a Normal approximation to binomial can be applied to approximate the distribution of p if the following conditions are satisfied:
- np ≥ 10
- n(1 - p) ≥ 10
Check the conditions as follows:
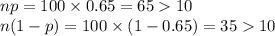
Thus, a Normal approximation to binomial can be applied.
So,
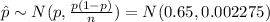 .
.
(1)
Compute the value of
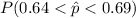 as follows:
as follows:
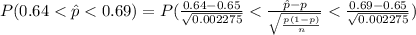

Thus, the probability that the sample percentage indicating global warming is having a significant impact on the environment will be between 64% and 69% is 0.3674.
(2)
Let
 and
and
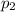 be the two population percentages that will contain the sample percentage with probability 90%.
be the two population percentages that will contain the sample percentage with probability 90%.
That is,
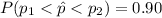
Then,
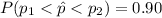
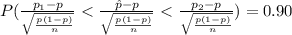
![P(-z<Z<z)=0.90\\P(Z<z)-[1-P(Z<z)]=0.90\\2P(Z<z)-1=0.90\\2P(Z<z)=1.90\\P(Z<z)=0.95](https://img.qammunity.org/2021/formulas/mathematics/college/7j06s6am0g2l41l1vic0pq3s6t5qotocun.png)
The value of z for P (Z < z) = 0.95 is
z = 1.65.
Compute the value of
 and
and
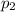 as follows:
as follows:
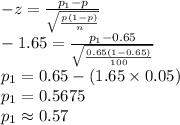
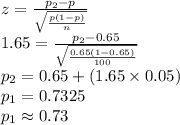
Thus, the two population percentages that will contain the sample percentage with probability 90% are 0.57 and 0.73.
(3)
Let
 and
and
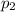 be the two population percentages that will contain the sample percentage with probability 95%.
be the two population percentages that will contain the sample percentage with probability 95%.
That is,
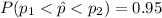
Then,
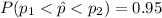
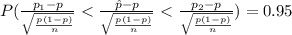
![P(-z<Z<z)=0.95\\P(Z<z)-[1-P(Z<z)]=0.95\\2P(Z<z)-1=0.95\\2P(Z<z)=1.95\\P(Z<z)=0.975](https://img.qammunity.org/2021/formulas/mathematics/college/kobehq2c9e491gkrvqtteqkd6titwd4yid.png)
The value of z for P (Z < z) = 0.975 is
z = 1.96.
Compute the value of
 and
and
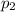 as follows:
as follows:
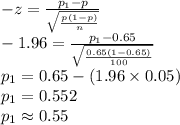
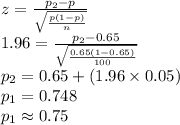
Thus, the two population percentages that will contain the sample percentage with probability 95% are 0.55 and 0.75.