Question

A parallel-plate capacitor has plates of area 0.30 m2 and a separation of 2.10 cm. A battery charges the plates to a potential difference of 190 V and is then disconnected. A dielectric slab of thickness 4 mm and dielectric constant 4.8 is then placed symmetrically between the plates.

(a) What is the capacitance before the slab is inserted?
(b) What is the capacitance with the slab in place?
(c) What is the free charge q before and after the slab is inserted?
(d) What is the magnitude of the electric field in the space between the plates and dielectric and in the dielectric itself?
(f) With the slab in place, what is the potential difference across the plates?
(g) How much external work is involved in inserting the slab?

Answer 1

a) 1.26e^-10F

b) 1.47e^-10F

c) 2.39e^-8C 2.89e^-8C

d) E=4500.94N/C

e) E'=5254.23N/C

f) 100.68V

g) 1.65e^-10J

Step-by-step explanation:

To compute the capacitance we can use the formula:

`C=(k\epsilon_o A)/(d)`

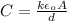
where k is the dielectric constant of the material between the plates. d is the distance between plates and A is the area.

(a) Before the material with dielectric constant is inserted we have that k(air)=1. Hence, we have:

`k=1\\A=0.30m^2\\d=0.021m\\e_o=8.85*10^(-12)C^2/(Nm^2)\\\\C=((1)(8.85*10^(-12)C^2/(Nm^2))(0.30m^2))/(0.021m)=1.26*10^(-10)F`

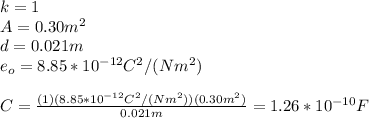
(b) With the slab we have that k=4.8 and the thickness is 4mm=4*10^{-3}m. In this case due to the thickness of the slab is not the same as d, we have to consider the equivalent capacitance of the series of capacitances:

`C=((1)/(C_1)+(1)/(C_2)+(1)/(C_1))\\\\\\C_1=((1)(8.85*10^(-12)C^2/(Nm^2))(0.30m^2))/(8.5*10^(-3)m)=3.1*10^(-10)F\\\\C_2=((4.8)(8.85*10^(-12)C^2/(Nm^2))(0.30m^2))/(4*10^(-3)m)=3.186*10^(-9)F\\\\C=1.47*10^(-10)F`

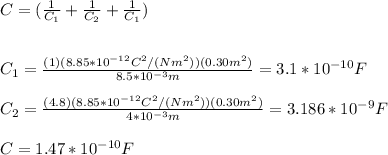
(c)

The charge between the plates for both cases, with the slab is given by:

Q : without the slab

Q': with the slab

`Q=CV=(1.26*10^(-10)F)(190V)=2.39*10^(-8)C\\\\Q'=C'V=(1.47*10^(-10F))(190V)=2.79*10^(-8)C\\`

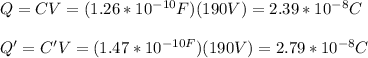
(d) The electric field between the plate is given by:

`E=(Q)/(2\epsilon_o A)`

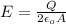
E: without the slab

E': with the slab

`E=(2.39*10^(-8)C)/(2(8.85*10^(-12)C^2/Nm^2)(0.30m^2))=4500.94N/C\\\\E'=(2.79*10^(-8)C)/(2(8.85*10^(-12)C^2/Nm^2)(0.30m^2))=5254.23N/C\\`

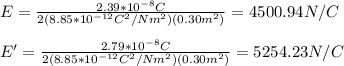
(f) We can assume the system as composed by V=V1+V'+V1 as in (c). By using the equation V=Ed we obtain:

`V=2(4500.94)(8.85*10^(-3)m)+(5254.23)(4*10^(-3)m)=100.68V`

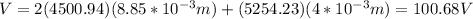
(g) External work is the difference between the energies of the capacitor before and after the slab is placed between the parallels:

`\Delta E=(1)/(2)[(1.26*10^(-10)F)(120V)-(1.47*10^(-10))(100.6V)]=1.65*10^(-10)J`