Question

Which point is on the circle centered at the origin with a radius of 5 units? Distance formula: StartRoot (x 2 minus x 1) squared + (y 2 minus y 1) squared EndRoot

Answer 1

A. (2,\sqrt{21})

Explanation:

Answer 2

Option A)
`(2,√(21))`

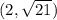
Explanation:

The following information is missing in the question:

A.
`(2,√(21))`

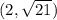
B.
`(2,√(23))`

C. (2, 1)

D. (2, 3)

We are given the following in the question:

A circle centered at origin and radius 5 units.

We have to find the equation of a point that lies on the circle.

Let (x,y) lie on the circle.

Distance formula:

`d = √((y_2-y_1)^2+(x_2-x_1)^2)`

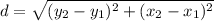
Putting

`(x_2,y_2) = (x,y)\\(x_1.y_1) = (0,0)\\d = 5`

We get,

`5 = √((y-0)^2 + (x-0)^2)\\√(x^2+y^2)=5\\x^2+y^2 = 25`

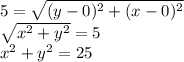
is the required equation of point on the circle centered at the origin with a radius of 5 units.

The point
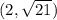`(2,√(21))` satisfies the given equation.

Verification:

`(2)^2 + (√(21))^2\\=4 + 21\\=25`

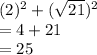
Thus,
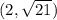`(2,√(21))` lies on the circle centered at the origin with a radius of 5 units.