Answer:
(a) H₀: P₂ - P₁ = 0 vs. Hₐ: P₂ - P₁ > 0.
(b) The critical value for the rejection region is 2.33.
(c) The calculated z-statistic value is, z = 7.17.
(d) The p-value of the test is 0.
(e) The proportion of women who view sexual harassment on the job is more than that for men.
Explanation:
Here we need to test whether the proportion of women who view sexual harassment on the job is more than that for men.
(a)
Our hypothesis will be:
H₀: The difference between the proportions of men and women who view sexual harassment on the job as a problem is same, i.e. P₂ - P₁ = 0
Hₐ: The difference between the proportions of men and women who view sexual harassment on the job as a problem is more than 0, i.e. P₂ - P₁ > 0.
(b)
The significance level of the test is:
α = 0.01
The rejection region is defined as:
If test statistic value, z
 > z₀.₀₁ then then null hypothesis will be rejected.
> z₀.₀₁ then then null hypothesis will be rejected.
Compute the critical value of the test as follows:
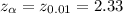
*Use z-table.
Thus, the critical value for the rejection region is 2.33.
(c)
The z-statistic for difference of proportions is,

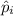 = ith sample proportion,
= ith sample proportion,
P = population proportion
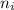 = ith sample size.
= ith sample size.
The given information is:

Since, there is no data about the population proportion the unbiased estimate of P is given by,
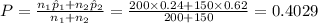
Using the given data we compute the z-statistic as:

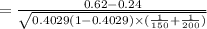
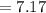
Thus, the calculated z-statistic value is, z = 7.17.
(d)
Compute the p-value of the test as follows:
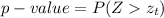
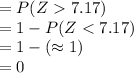
Thus, the p-value of the test is 0.
(e)
As stated in part (b), if z₀.₀₁ > z
 then then null hypothesis will be rejected.
then then null hypothesis will be rejected.
z
 = 7.17 > z₀.₀₁ = 2.33
= 7.17 > z₀.₀₁ = 2.33
Thus, the null hypothesis will be rejected at 1% level of significance.
Conclusion:
The proportion of women who view sexual harassment on the job is more than that for men.