Answer: A
Explanation:
We need to get the denominators to be same first before we can do anything to the numerator.
The LCD (lowest common denominator) is
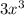 . To find the LCD, multiply the denominators together:
. To find the LCD, multiply the denominators together:
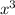 ·
·
 =
=
 .
.
Below, we are trying to get the denominators to equal the same or to
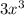 .
.
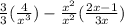
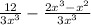
Now that the denominators are the same, we can subtract the numerators from each other.
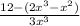
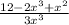
Now, we can just reorganize the variables.
Answer: A or
