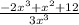Question

What is the difference of the rational expressions below?

Answer 1

Answer: A

Explanation:

We need to get the denominators to be same first before we can do anything to the numerator.

The LCD (lowest common denominator) is
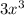`3x^(3)`. To find the LCD, multiply the denominators together:
`x^(3)` ·
`3x` =
`3x^{3`.

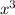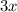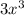Below, we are trying to get the denominators to equal the same or to
`3x^(3)`.

`(3)/(3) ((4)/(x^(3) ) ) - (x^(2) )/(x^(2) ) ((2x-1)/(3x) )`

`(12)/(3x^(3) ) - (2x^(3)-x^(2) )/(3x^(3) )`

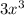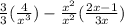
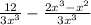
Now that the denominators are the same, we can subtract the numerators from each other.

`( 12 - (2x^(3) -x^(2))\\)/(3x^(3) ) \\`

`(12-2x^(3) +x^(2) )/(3x^(3) )`

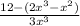
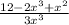
Now, we can just reorganize the variables.

Answer: A or
`(-2x^(3) + x^(2)+12 )/(3x^(3) )`