Answer:
4 cm.
Explanation:
Given:
A box has a volume of 308 cm cubed.
Its height is 4 cm greater than its length.
Its length is 3 cm greater than its width.
Question asked:
What is the width of the box?
Solution:
Let width =

Length =
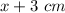
Height =

As we know:
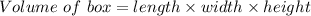

As width can never be in negative,

By substituting the value:-
Width =
 = 4 cm
= 4 cm
Thus, width of the box is 4 cm.