Question

A long coaxial cable consists of an inner cylindrical conductor with radius a and an outer coaxial cylinder with inner radius b and outer radius c. The outer cylinder is mounted on insulating supports and has no net charge. The inner cylinder has a uniform positive charge per unit length λ.

1. Calculate the electric field (a) at any point between the cylinders a distance r from the axis and (b) at any point outside the outer cylinder.

Answer 1

(a) E=λ/(2\pi e0 r)

(b) E = 0

Step-by-step explanation:

(a) We can use the Gaussian's Law to calculate the electric field at any distance r from the axis. By using a cylindrical Gaussian surface we have:

`\int \vec{E}\cdot d\vec{r}=(\lambda)/(\epsilon_o)`

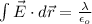
where λ is the total charge per unit length inside the Gaussian surface. In this case we have that the Electric field vector is perpendicular to the r vector. Hence:

`E\int dr=E2\pi r=(\lambda)/(\epsilon_o)\\\\E=(\lambda)/(2\pi r \epsilon_o)`

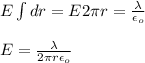
(b) outside of the outer cylinder there is no net charge inside the Gaussian surface, because charge of the inner radius cancel out with the inner surface of the cylindrical conductor.

Hence, we have that E is zero.

hope this helps!!

Answer 2

1a. E(r) = lambda/ 2πrEo

1b. Electric field outside the outside cylinder = lambda/ 2πrEo

Step-by-step explanation: