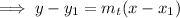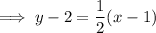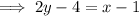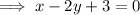Question

Find the equation of the tangent to the circle whose equation is given below at the point (1,2)

(x-3)^2 + (y+2)^2 = 20

give answer in form ax+by+c=0 where abc are integers

Answer 1

`x-2y+3=0`

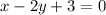
Explanation:

Equation of a circle:
`(x-h)^2+(y-k)^2=r^2`

(where (h, k) is the centre, and r is the radius)

Given equation:
`(x-3)^2+(y+2)^2=20`

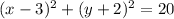
Therefore, the centre is (3, -2) and the radius is √20

To find the equation of the tangent

The tangent of a circle is perpendicular to the radius at the point.

Therefore, first find the gradient (slope) of the line that passes through the centre of the circle and the given point.

`\textsf{let}\:(x_1,y_1)=(1,2)`

`\textsf{let}\:(x_2,y_2)=(3,-2)`

`\textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(-2-2)/(3-1)=-2`

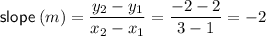
If two lines are perpendicular to each other, the product of their gradients will be -1.

Therefore, the gradient of the tangent is:

`m_t \cdot-2=-1\implies m_t=\frac12`

Now use the point-slope formula of a linear equation to find the equation of the tangent:

`\implies y-y_1=m_t(x-x_1)`

`\implies y-2=\frac12(x-1)`

`\implies 2y-4=x-1`

`\implies x-2y+3=0`