Question

Can someone please help me with this calculus problem? I am very confused on how to complete it.

Divide a 14-in diameter pizza into three slices of the equal area using two parallel cuts.
Approximate approach: use Riemann sums to estimate where to place the cuts

Answer 1

9514 1404 393

Answer:

cut the pizza ±1.855 inches from the centerline

Explanation:

Here's an interesting approach that actually gives amazing accuracy.

If the pizza were a 14" square, the cuts would be 14/6 = 2.33 inches from the centerline. If we draw a diagram of the pizza as a circle of radius 7 centered at the origin, we propose to create a running total of the areas of trapezoidal slices in the first quadrant parallel to the y-axis out to a distance of x=2.3. We want to find where the accumulated area is close to 1/12 of the area of the circle. In order to get sufficient resolution as to where the cut should be, we choose to use a total of 20 slices to cover that area. (n=20 for the Riemann sum)

Of course, the equation of the circle is x^2 +y^2 = 49. Then the value of y of interest is ...

f(x) = √(49 -x^2)

where the value of x is some multiple of 2.3/20, the slice width for our Riemann sum. If we number the slices 0 to 19, the accumulated area up to slice k is ...

`\displaystyle A_k=(2.3)/(20)\sum_(n=0)^(k)(f(x_n)+f(x_(n+1)))/(2)`

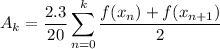
As you can tell, this is using the trapezoidal method of computing the Riemann sum. We considered left, right, and midpoint integration methods but settled on this as having the kind of accuracy we wanted.

We want an accumulated area of 1/3 of our quarter circle, or (1/12)(π)(7^2) = 49π/12, so we want to find the zero of the difference Ak -49π/12.

As it turns out, the desired area is bracketed by k=16 and k=17. By linearly interpolating between the area values for these numbers of slices, we find that x=1.8546 is the location we need to cut the pizza. The problem is symmetrical, so the other cut is at x = -1.8546 inches from center.

_____

When evaluating functions multiple times, it is convenient to use a graphing calculator or spreadsheet. With a spreadsheet, you could list function values in one column, the trapezoidal method area in another column, and the accumulated area in yet another column. As here, the interpolation required for a final answer is also easily handled in a spreadsheet.

__

Additional comment

The arc α that encloses a sector equal to 1/3 the area of the pizza will satisfy the equation α -sin(α) -2π/3 = 0. That is about 2.6053256746 radians. The cut distance we're trying to find is the 7cos(α/2) ≈ 1.85452459222 inches, which differs by about 0.005% from the value we found.