Question

Two carts, one twice as heavy as the other, are at rest on a horizontal track. A person pushes each cart for 8 s. Ignoring friction and assuming equal force exerted on both carts, the kinetic energy of the heavy cart after the push compared to the kinetic energy of the light cart is:______.

A) 1/4 K.
B) 1/2 K.
C) K.
D) 2K.
E) 4K.

Answer 1

The correct option is: B that is 1/2 K

Step-by-step explanation:

Given:

Two carts of different masses, same force were applied for same duration of time.

Mass of the lighter cart =
`m`

Mass of the heavier cart =
`2m`

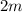
We have to find the relationship between their kinetic energy:

Let the KE of cart having mass m be "K".

and KE of cart having mass m be "K1".

As it is given regarding Force and time so we have to bring in picture the concept of momentum Δp and find a relation with KE.

Numerical analysis.

⇒
`KE = (mv^2)/(2)`

⇒
`KE = (mv^2)/(2)* (m)/(m)`

⇒
`KE = (m^2v^2)/(2)* (1)/(m)`

⇒
`KE = ((mv)^2)/(2)* (1)/(m)`

⇒
`KE = ((\triangle p)^2)/(2)* (1)/(m)`

⇒
`KE = ((\triangle p)^2)/(2m)=((F* t)^2)/(2m)`

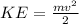
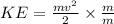
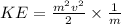
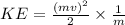
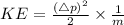
Now,

Kinetic energies and their ratios in terms of momentum or impulse.

KE (K) of mass m.

⇒
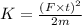`K=((F* t)^2)/(2m)` ...equation (i)

KE (K1) of mass 2m.

⇒
`K_1=((F* t)^2)/(2* 2m)`

⇒
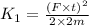
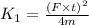`K_1=((F* t)^2)/(4m)` ...equation (ii)

Lets divide K1 and K to find the relationship between the two carts's KE.

⇒
`(K_1)/(K) =((F* t)^2)/(4m) * (2m)/((F* t)^2)`

⇒
`(K_1)/(K) =(2m)/(4m)`

⇒
`(K_1)/(K) =(2)/(4)`

⇒
`(K_1)/(K) =(1)/(2)`

⇒
`K_1=(K)/(2)`

⇒
`K_1=(1)/(2)K`

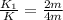
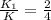
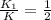
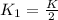
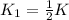
The kinetic energy of the heavy cart after the push compared to the kinetic energy of the light cart is 1/2 K.