Answer:
Part A)
t(1) > t(2), the stone thrown 30 above the horizontal spends more time in the air.
Part B)
x(f1) > x(f2), the first stone will land farther away from the building.
Step-by-step explanation:
Part A)
Let's use the parabolic motion equation to solve it. Let's define the variables:
- y(i) is the initial height, it is a constant.
- y(f) is the final height, in our case is 0
- v(i) is the initial velocity (v(i)=16 m/s)
- θ1 is the first angle, 30°
- θ2 is the first angle, -30°
For the first stone
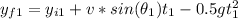
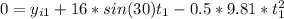
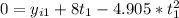 (1)
(1)
For the second stone
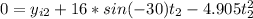
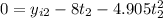 (2)
(2)
If we solve the equation (1) we will have:
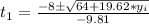
We can do the same procedure for the equation (2)
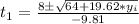
We can analyze each solution to see which one spends more time in the air.
It is easy to see that the value inside the square root of each equation is always greater than 8, assuming that the height of the building is > 0. Now, to get positive values of t(1) and t(2) we need to take the negative option of the square root.
Therefore, t(1) > t(2), it means that the stone thrown 30 above the horizontal spends more time in the air.
Part B)
We can use the equation of the horizontal position here.
First stone
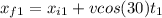
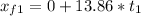
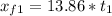
Second stone
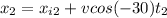
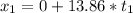
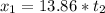
Knowing that t(1) > t(2) then x(f1) > x(f2)
Therefore, the first stone will land farther away from the building.
They land at different points at different times.
I hope it helps you!