Question

Suppose that on a true/false exam you have no idea at all about the answers to three questions. You choose answers randomly and therefore have a 50–50 chance of being correct on any one question. Let CCW indicate that you were correct on the first two questions and wrong on the third, let WCW indicate that you were wrong on the first and third questions and correct on the second, and so forth. a. List the elements in the sample space whose outcomes are all possible sequences of correct and incorrect responses on your part. b. Write each of the following events as a set and find its probability: (i) The event that exactly one answer is correct. (ii) The event that at least two answers are correct. (iii) The event that no answer is correct.

Answer 1

a.

`\text{Sample Space} = \{ CCC,CCW,CWW,WWW,WWC,WCC,WCW,CWC \}`

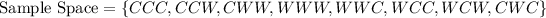
b.

(i) 1/2

(ii) 2/3

(iii) 1/6

Explanation:

a.

The sample space is the list of all possibilities.

`\text{Sample Space} = \{ CCC,CCW,CWW,WWW,WWC,WCC,WCW,CWC \}`

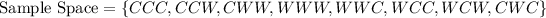
b.

(i)

If exactly one answer is correct the favorable outcomes are

CWW , WCW , WWC.

And the probability would be 3/6 = 1/2.

(ii)

If at least two answers are correct then the favorable outcomes are

CCC,CCW,WCC,CWC

and the probability is 4/6 = 2/3.

(iii)

If no answer is correct, the favorable outcomes are

WWW

and the probability is 1/6.