Question

How does the resistance in the circuit impact the height and width of the resonance curve? (If the resistance were to increase would the height change? Would the width? If so, how?)

Answer 1

The reactances vary with frequency, with large XL at high frequencies and large Xc at low frequencies, as we have seen in three previous examples. At some intermediate frequency fo, the reactances will be the same and will cancel, giving Z = R; this is a minimum value for impedance and a maximum value for Irms results. We can get an expression for fo by taking

XL=Xc

Substituting the definitions of XL and XC,

2
`\pi`foL=1/2
`\pi`foC

Solving this expression for fo yields

fo=1/2
`\pi`
`√(LC)`

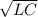
where fo is the resonant frequency of an RLC series circuit. This is also the natural frequency at which the circuit would oscillate if it were not driven by the voltage source. In fo, the effects of the inductor and capacitor are canceled, so that Z = R and Irms is a maximum.

Step-by-step explanation:

Resonance in AC circuits is analogous to mechanical resonance, where resonance is defined as a forced oscillation, in this case, forced by the voltage source, at the natural frequency of the system. The receiver on a radio is an RLC circuit that oscillates best at its {f} 0. A variable capacitor is often used to adjust fo to receive a desired frequency and reject others is a graph of current versus frequency, illustrating a resonant peak at Irms at fo. The two arcs are for two dissimilar circuits, which vary only in the amount of resistance in them. The peak is lower and wider for the highest resistance circuit. Thus, the circuit of higher resistance does not resonate as strongly and would not be as selective in a radio receiver, for example.

A current versus frequency graph for two RLC series circuits that differ only in the amount of resistance. Both have resonance at fo, but for the highest resistance it is lower and wider. The conductive AC voltage source has a fixed amplitude Vo.