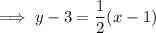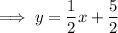Answer:
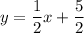
Explanation:
M = (-1, 7)
N = (3, -1)
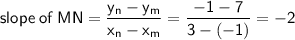
If two lines are perpendicular to each other, the product of their slopes will be -1. Therefore, the slope (m) of the line perpendicular to MN is:

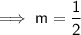
If the line bisects the line MN, it will intersect it at the midpoint of MN:
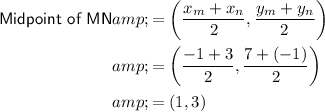
Finally, use the point-slope form of the linear equation with the found slope and the midpoint of MN: