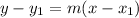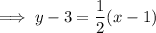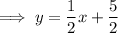Question

The line MN is shown on the grid.
Find the equation of the perpendicular bisector of line MN.

Answer 1

`y=\frac12x+\frac52`

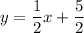
Explanation:

M = (-1, 7)

N = (3, -1)

`\sf slope\:of\:MN=(y_n-y_m)/(x_n-x_m)= (-1-7)/(3-(-1))=-2`

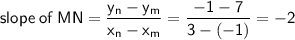
If two lines are perpendicular to each other, the product of their slopes will be -1. Therefore, the slope (m) of the line perpendicular to MN is:

`\sf \implies -2 * m=-1`

`\sf \implies m=\frac12`

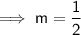
If the line bisects the line MN, it will intersect it at the midpoint of MN:

`\begin{aligned}\textsf{Midpoint of MN} & =\left((x_m+x_n)/(2),(y_m+y_n)/(2)\right)\\ & =\left((-1+3)/(2),(7+(-1))/(2)\right)\\ & =(1,3)\end{aligned}`

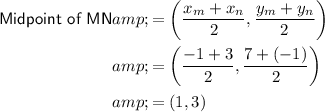
Finally, use the point-slope form of the linear equation with the found slope and the midpoint of MN:

`y-y_1=m(x-x_1)`

`\implies y-3=\frac12(x-1)`

`\implies y=\frac12x+\frac52`

Answer 2

Find midpoint coordinates:

`\rightarrow \sf ((-1+3)/(2) ), \ ((7+(-1))/(2) )`

`\hookrightarrow \sf (1, \ 3)`

Find the gradient of MN:

`\dashrightarrow \sf (-1-7)/(3-(-1))`

`\dashrightarrow \sf -2`

slope of perpendicular bisector:

`\rightarrow \sf (1)/(2)`

Equation:

`\sf \rightarrow y = (1)/(2)x+(5)/(2)`