Question

In order to estimate the average time spent on the computer terminals per student at a local university, data were collected for a sample of 81 business students over a one-week period. Assume the population standard deviation is 1.8 hours. Answer questions 7 - 9.

7. What is the standard error of the mean?

a. 7.50
b . 0.39
c. 2.00
d. 0.20

8. With a 0.95 probability, the margin of error is approximately

a. 0.39
b 1.96
c. 0.20
d. 1.64

9. If the sample mean is 9 hours, then the 95% confidence interval is

a. 7.04 to 10.96 hours
b. 7.36 to 10.64 hours
c. 7.80 to 10.20 hours
1d. 8.61 to 9.39 hours

Answer 1

7) d)

standard error of the mean of one sample of 'n' observation = 0.20

8) a)

The margin of Error = 0.392

9) d

The 95% of confidence intervals are (8.61 , 9.39)

Explanation:

7)

solution:-

The Given data sample size 'n' = 81

Given Population standard deviation 'σ' = 1.8 hours

The standard error of the mean of one sample of 'n' observation is

Standard error (SE)

=
`(S.D)/(√(n) )`

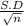
= σ / √n

=
`(1.8)/(√(81) ) =0.2`

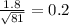
standard error of the mean of one sample of 'n' observation = 0.20

8)

Solution:-

The Given data sample size 'n' = 81

Given Population standard deviation 'σ' = 1.8 hours

Given the probability is 0.95

The z- score = 1.96 at 0.05 level of significance.

The margin of Error =
`(z_(0.95) S.D)/(√(n) )`

=
`(1.96 (S.D))/(√(n) )`

=
`(1.96 (1.8))/(√(81) )`

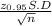
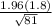
= 0.392

The margin of Error = 0.392

9)

Solution:-

The 95% of confidence intervals are

`(x^(-) - 1.96(S.D)/(√(n) ) , x^(-) + 1.96(S.D)/(√(n) ) )`

`(9 - 1.96(1.8)/(√(81) ) , 9+ 1.96(1.8)/(√(81) ) )`

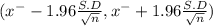
(9 - 0.392 , (9 + 0.392)

(8.609 , 9.392)

The 95% of confidence intervals are (8.61 , 9.39)