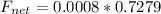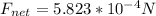Question

A turntable is off and is not spinning. A 0.8 g ant is on the disc and is 9 cm away from the center. The turntable is turned on and 0.8 s later it has an angular speed of 45 rpm. Assume the angular acceleration is constant and determine the following quantities for the ant 0.4 s after the turntable has been turned on. Express all quantities using appropriate mks units.

Answer 1

Complete Question

The complete is shown on the first uploaded image

Answer:

`\alpha = 5.89 rad/s^2`

`w__(0.4)}= 2.36 \ rad/s`

`v= 0.212m/s`

`a_t= 0.5301 m/s`

`a_r = 0.499 m/s`

`a = 0.7279 m/s`

`F_(net)=5.823*10^(-4)N`

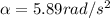
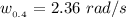
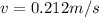
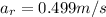
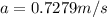
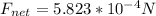
Step-by-step explanation:

From the question we are told that

mass of the ant is
`m_a = 0.8g = (0.8)/(1000) = 0.00018kg`

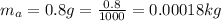
The distance from the center is
`d = 9cm = (9)/(100) = 0.09m`

The angular speed is
`w = 45rpm = 45 * (2 \pi )/(60) = 1.5 \pi`

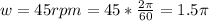
The time taken to attain angular acceleration of 45rpm
`t_1 = 0.8s`

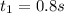
The time taken is
`t_2 = 0.4 s`

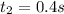
The angular acceleration is mathematically represented as

`\alpha = (w)/(t)`

`= (1.5)/(0.8)`

`\alpha = 5.89 rad/s^2`

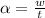
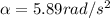
The angular velocity at time t= 0.4s is mathematically represented as

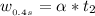`w__(0.4s)} = \alpha * t_2` Recall angular acceleration is constant

`= 5.89 * 0.4`

`w__(0.4)}= 2.36 \ rad/s`

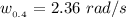
The linear velocity is mathematically represented as

`v = w__(t_2)} * r`

`= 2.36 * 0.09`

`v= 0.212m/s`

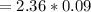
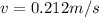
The tangential acceleration is mathematically represented as

`a_(t) = \alpha * r`

`= 5.89 * 0.09`

`a_t= 0.5301 m/s`

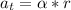
The radial acceleration is mathematically represented as

`a_r = (v^2)/(r)`

`= (0.212^2)/(0.09)`

`a_r = 0.499 m/s`

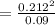
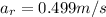
The resultant velocity is mathematically represented as

`a = √(a_t^2 + a_r^2)`

`= √(0.53^2 + 0.499^2)`

`a = 0.7279 m/s`

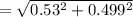
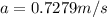
The net force is mathematically represented as

`F_(net) = 0.0008 * 0.7279`

`F_(net)=5.823*10^(-4)N`