Question

A 1.0 m long piece of coaxial cable has a wire with a radius of 1.1 mm and a concentric conductor with inner radius 1.3 mm. The area between the cable and the conductor is filled with a dielectric. If the voltage drop across the capacitor is 6000 V when the line charge density is 8.8 μC/m, find the value of the dielectric constant. (k = 1/4πε₀ = 8.99 × 109 N · m²/C²)A) 4.8

B) 5.3
C) 4.4
D) 5.7

Answer 1

C) 4.4

Step-by-step explanation:

The potential of a cylindrical capacitor is given by the formula:

`V=(2kq)/(L\epsilon)ln((a)/(b))\\\\\epsilon=(2kq)/(LV)ln((a)/(b))`

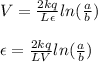
where:

k : Coulomb Constant

L : length of the capacitor

a : outer radius

b : inner radius

V : potential

By replacing we obtain:

`\epsilon=(2(8.89*10^(9)N/m^2C^2)(8.8*10^(-6)C))/((1m)(6000V))ln((1.3mm)/(1.1mm))=4.35`

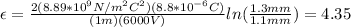
Hence, the answer is C) 4.4 (4.35 is approximately 4.4)

hope this helps!!