Question

Find the measure of Q, the smallest angle in the triangle whose sides have lengths 4-5, and 6. Round the measure to the nearest whole degree.

Answer 1

Answer:c) 41

Explanation:

Answer 2

Given:

Given that PQR is a triangle.

The measures of the sides of the triangle are 4,5 and 6.

We need to determine the measure of ∠Q.

Measure of ∠Q:

The measure of ∠Q can be determined using the law of cosines formula.

Thus, we have;

`\cos (Q)=(p^(2)+r^(2)-q^(2))/(2 p r)`

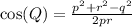
Substituting p = 6, q = 4, r = 5, we get;

`\cos (Q)=(6^(2)+5^(2)-4^(2))/(2 (6)(5))`

Simplifying, we get;

`\cos (Q)=(36+25-16)/(2 (30))`

`\cos (Q)=(45)/(60)`

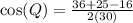
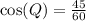
Dividing, we get;

`\cos (Q)=0.75`

`Q=cos^(-1)(0.75)`

`Q=41^(\circ)`

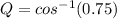
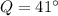
Thus, the measure of ∠Q is 41°

Hence, Option b is the correct answer.