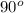Answer:
Explanation:
since AD is a median it implies that triangle ABC is bisected to two equal right angled triangle which are ADB and ADC.
FE is parrallel to BC and cuts AB at F and AC at E shows that there are two similar triangles formed which are AFE and ABC.
Recall that ADC is a right angled triangle, ED bisects a right angled triangle the the ADE =
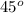 .
.
Now, Let FD bisect angle ADB,
then ADF =
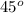 too.
too.
Since AFX is similar to Triangle ABD and that Triangle AEX is similar to Triangle ACD, then EDX is similar to FDX
FDE = ADF + ADE =