Question

An article in the Journal of Materials Engineering (Vol 11, No. 4, 1989, pp. 275-282) reported the results of an experiment to determine failure mechanisms for plasma-sprayed thermal barrier coatings. The failure stress for one particular coating (NiCrAlZr) under two different test conditions is as follows:

Failure stress ( times 10^6 Pa) after nine 1-hr cycles: 19.8, 18.5, 17.6,16.7, 16.7, 14.8, 15.4, 14.1, 13.6
Failure stress ( times 10^6 Pa) after six 1-hr cycles: 14.9, 12.7, 11.9, 11.4, 10.1,7.9
(a) What assumptions are needed to construct confidence intervals for the difference in mean failure stress under the two different test conditions? Use normal probability plots of the data to check these assumptions.
(b) Perform a hypothesis test to determine if the mean failure stress of the two different test conditions is the same at the 0.05 significance level.
(c) Confirm that the P-value of this test is 0.001.

Answer 1

Explanation:

Hello!

You have two variables of interest

X₁: failure stress of a NiCrAlZr coating after nine 1-hr cycles.

X₂: failure stress of a NiCrAlZr coating after six 1-hr cycles.

a)

To be able to estimate the difference between the means using a confidence interval, you need that both variables have a normal distribution and to determine whether or not the population variances are equal.

If the population variances are equal, σ₁²=σ₂², you can use a pooled variance t-test

If the population variances are different, σ₁²≠σ₂², you have to use Welch's t-test

Using α: 0.05

The normality test for X₁ shows a p-value of 0.7449 ⇒ You can assume it has a normal distribution.

The normality test for X₂ shows a p-value of 0.9980 ⇒ You can assume it has a normal distribution.

The F-test for variance homogeneity shows a p-value of 0.6968 (H₀:σ₁²=σ₂²) ⇒You can assume both population variances are equal.

b) and c)

You need to test if both population means are the same, the hypotheses are:

H₀: μ₁=μ₂

H₁: μ₁≠μ₂

α: 0.05

`t= \frac{(X[bar]_1-X[bar]_2)-(Mu_1-Mu_2)}{Sa*\sqrt{(1)/(n_1) +(1)/(n_2) } } ~~t_(n_1+n_2-2)`

`Sa= \sqrt{((n_1-1)S^2_1+(n_2-1)S^2_2)/(n_1+n_2-2) } = \sqrt{(8*4.28+5*5.62)/(9+6-2) }= √(4.7953)= 2.189= 2.19`

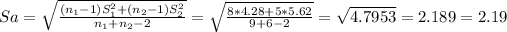
`t_(H_0)= \frac{(X[bar]_1-X[bar]_2)-(Mu_1-Mu_2)}{Sa*\sqrt{(1)/(n_1) +(1)/(n_2) } } = \frac{(16.36-11.48)-0}{2.19*\sqrt{(1)/(9) +(1)/(6) } } = 4.23`

The distribution of this test is a t with 13 degrees of freedom and the test is two-tailed, so to calculate the p-value you have to do the following:

P(t₁₃≤-4.23)+P(t₁₃≥4.23)= P(t₁₃≤-4.23)+[1-P(t₁₃<4.23)]= 0.000492 + (1-0.999508)= 2*0.000492= 0.000984≅ 0.001

The p-value: 0.001 is less than α: 0.05, the decision is to reject the null hypothesis.

I hope it helps!