Answer:
Therefore she invested $10600 and $4000 in Fund A and Fund B respectively.
Explanation:
Given that,
Jenelle invested $14600 in two mutual funds.
Fund A 5% profit during the first year.
Fund B suffered a 2.5% loss.
Let she invested $x in Fund A.
Then the amount of remaining money is =$(14600-x)
So, she invested $(14600-x) in fund B.
Since Fund A 5% profit during the first year.
The amount of profit from fund A is
= Invest amount in fund A × 5%
=
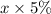
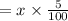

Since Fund B suffered a 2.5% loss.
The amount of loss in fund B is
=Invest amount in fund B ×2.5%
=(14600-x)×2.5%
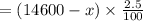
Total profit
= Amount of profit - Amount of loss
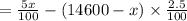



According to the problem,
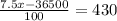
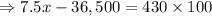
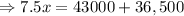
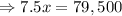
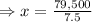
⇒x=10,600
She invested in fund B = $(14600-10600)=$4000
Therefore she invested $10600 and $4000 in Fund A and Fund B respectively.