Answer:
Approximately
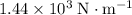 assuming that the spring has zero mass.
assuming that the spring has zero mass.
Step-by-step explanation:
Without any external force, a piece of mass connected to an ideal spring (like the chair in this question) will undergo simple harmonic oscillation.
On the other hand, the force constant of a spring (i.e., its stiffness) can be found using Hooke's Law. If the spring exerts a restoring force
 when its displacement is
when its displacement is
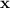 , then its force constant would be:
, then its force constant would be:
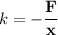 .
.
The goal here is to find the expressions for
 and for
and for
 . By Hooke's Law, the spring constant would be ratio of these two expressions.
. By Hooke's Law, the spring constant would be ratio of these two expressions.
Let
 represent the time period of this oscillation. With the chair alone, the period of oscillation is
represent the time period of this oscillation. With the chair alone, the period of oscillation is
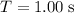 .
.
For a simple harmonic oscillation, the angular frequency
 can be found from the period:
can be found from the period:
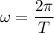 .
.
Let
 stands for the amplitude of this oscillation. In a simple harmonic oscillation, both
stands for the amplitude of this oscillation. In a simple harmonic oscillation, both
 and
and
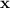 are proportional to
are proportional to
 . Keep in mind that the spring constant
. Keep in mind that the spring constant
 is simply the opposite of the ratio between
is simply the opposite of the ratio between
 and
and
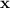 . Therefore, the exact value of
. Therefore, the exact value of
 shouldn't really affect the value of the spring constant.
shouldn't really affect the value of the spring constant.
In a simple harmonic motion (one that starts with maximum displacement and zero velocity,) the displacement (from equilibrium position) at time
 would be:
would be:
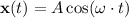 .
.
The restoring velocity at time
 would be:
would be:
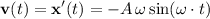 .
.
The restoring acceleration at time
 would be:
would be:
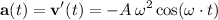 .
.
Assume that the spring has zero mass. By Newton's Second Law of motion, the restoring force at time
 would be:
would be:
 .
.
Apply Hooke's Law to find the spring constant,
 :
:
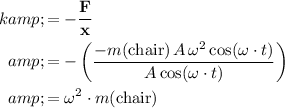 .
.
Again,
 stands for the angular frequency of this oscillation, where
stands for the angular frequency of this oscillation, where
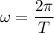 .
.
Before proceeding, note how
 was eliminated from the ratio (as expected.) Additionally,
was eliminated from the ratio (as expected.) Additionally,
 is also eliminated from the ratio. In other words, the spring constant is "constant" at all time. That agrees with the assumption that this spring is indeed ideal. Back to
is also eliminated from the ratio. In other words, the spring constant is "constant" at all time. That agrees with the assumption that this spring is indeed ideal. Back to
 :
:
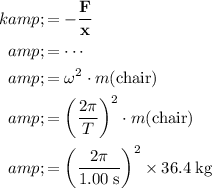 .
.
Side note on the unit of
 :
:
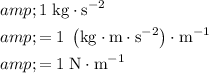 .
.