Answer:
(a) The confidence level desired by the researchers is 95%.
(b) The sampling error is 0.002 microcurie per millilitre.
(c) The sample size necessary to obtain the desired estimate is 25.
Explanation:
The mean and standard deviation of the amount of the radioactive element, cesium-137 present in a sample of n = 16 lichen specimen are:
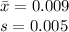
Now it is provided that the researchers want to increase the sample size in order to estimate the mean μ to within 0.002 microcurie per millilitre of its true value, using a 95% confidence interval.
The (1 - α)% confidence interval for population mean (μ) is:

(a)
The confidence level is the probability that a particular value of the parameter under study falls within a specific interval of values.
In this case the researches wants to estimate the mean using the 95% confidence interval.
Thus, the confidence level desired by the researchers is 95%.
(b)
In case of statistical analysis, during the computation of a certain statistic, to estimate the value of the parameter under study, certain error occurs which are known as the sampling error.
In case of the estimate of parameter using a confidence interval the sampling error is known as the margin of error.
In this case the margin of error is 0.002 microcurie per millilitre.
(c)
The margin of error is computed using the formula:

The critical value of z for 95% confidence level is:
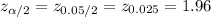
*Use a z-table.

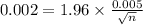
![n=[(1.96* 0.005)/(0.002)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/ond0u8fr6iwqkyjb7lz5i9v659mqp14rm2.png)
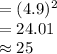
Thus, the sample size necessary to obtain the desired estimate is 25.