Answer:
0.748 ft (nearest thousandth)
Explanation:
Use the tan trig ratio:
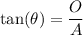
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
Given:
 = 14°
= 14°- O = x
- A = 3 ft

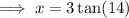
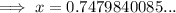
Therefore, the ladder reaches up the wall 0.748 ft (nearest thousandth)