Question

Find the area of the shaded region. Round to the nearest hundredth where necessary. Remember: you are subtracting the areas.

Answer 1

Given:

The base of the given figure = 23.8 ft

Height of the parallelogram = 15 ft

To find the area of the shaded region.

Formula

• 
  `A = A_(1) -A_(2)`

where,
`A` be the area of the shaded region

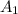`A_(1)` be the area of the parallelogram.

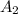`A_(2)` be the area of the triangular part.

• The area of triangle
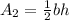  `A_(2) = (1)/(2) bh` where, b be the base and h be the height.

• The area of the parallelogram
  `A_(1) =( base)(height)`

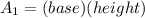
• By Pythagoras theorem,
  `hypotenuse^(2) = base^(2)+height^(2)`

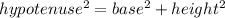
Now,

Putting, Base = 21, Hypotenuse = 23.8 we get,

`Height^(2) = 23.8^(2)-21^(2)`

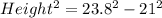
or,
`Height = √(566.44-441)`

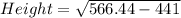
or,
`Height = 11.2`

Therefore,

Area of the parallelogram
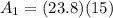`A_(1) = (23.8)(15)` sq ft = 357 sq ft

Area of the triangle
`A_(2)` =
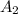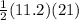`(1)/(2)(11.2)(21)` sq ft = 117.6 sq ft

So,

The area of the shaded part = (357-117.6) sq ft = 239.4 sq ft

Hence,

The area of the shaded part is 239.4 sq ft.