Question

Two rods are made of brass and have the same length. The cross section of one of the rods is circular, with a diameter of 2a. The other rod has a square cross section, where each side of the square is a length 2a. One end of the rods is attached to an immovable fixture which allows the rods to hang vertically. To the free end of each rod, a block of mass m is attached. Which rod, if either, will stretch more after the block is attached?

A. The one with the circular cross section will stretch more.

B. The one with the square cross section will stretch more.

C. Both will stretch by the same amount.

D. One cannot say which will stretch more without knowing the numerical values of a and m.

Answer 1

The correct option is;

A. The one with the circular cross section will stretch more.

Step-by-step explanation:

Here we have the cross section as being

1. Circular, with diameter, D = 2·a

2. Square cross section with each side length = 2·a

The area of the circular rod is then

Area of circle = π·D²/4 which is equal to

π×(2·a)²/4 = π·4·a²/4 = π·a²

The area of the rod with square cross section is

Area of square = Side² which gives

Area of cross section = (2·a)² = 4·a²

Therefore, since π = 3.142, the cross sectional area of the circular rod is less than that of the one with a square cross section

That is, π·a² = 3.142·a² < 4·a²

We note that the elongation or extension is directly proportional to the force applied as shown as follows

`(P)/(A) = E(\delta)/(L)`

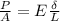
Where:

P/A = Force and

δ = Extension

The force is inversely proportional to the area, therefore a rod with less cross sectional area experiences more force and more elongation.

Answer 2

A. The one with the circular cross section will stretch more.

Step-by-step explanation:

According to the given data:

Two rods are made of brass and have the same length

Both rods having circular and square cross-section

Diameter of circular cross-section given is 2 a

therefore, Cross-section =
`A_c=(\pi (2a)^2)/(4)=\pi a^2`

If the length of square=2 a

then, Cross-section =
`A_(s)` = (2a)²=>4a²

Change in Length of rod = PL / AE

δL
`\alpha (1)/(A)`

Now, we are considering other factors same

the area of cross-section of square rod is more than Area of cross-section of circular rod

thus, the one with the circular cross section will stretch more