Question

The first term of a geometric sequence is 2, and the common ratio is 3. What is the 8th term of the sequence?

Answer 1

The 8th term of the sequence is 4374.

Explanation:

It is given that,

• The first term of a geometric sequence is 2, and the common ratio is 3.
• You need to find the 8th term of the sequence.

The general form of geometric sequence is a, ar, ar²,ar³,.......

where,

• a is the first term of the sequence. Here, the first term a = 2
• r is the common ratio. Here, the common ratio r = 3.

The formula to find the nth term of the geometric sequence is given by :

⇒
`n_(th) term = ar^(n-1)`

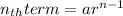
The question is asked to find the 8th term. Hence n = 8.

⇒
`8_(th) term = 2 * 3^(8-1)`

⇒
`2 * 3^(7)`

⇒
`2 * 2187`

⇒
`4374`

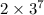
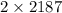
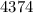
∴ The 8th term of the sequence is 4374.